SM2 算法原理

SM2 算法是国密标准的非对称算法标准，基于 ecc（Elliptic Curves Cryptography，椭圆曲线密码编码学）的扩展。提起非对称加密，自然想到了 RSA，对极大整数做因数分解的难度决定了RSA算法的可靠性（RSA 算法理解），这是 RSA 安全的基础。那国密加解密的算法基础是什么？首先我们先理解一下椭圆曲线。

SM2 椭圆曲线

国密 SM2 的算法基础是椭圆曲线，公式：

$$y^2=x^3+ax+b(4a^3+27b^2\ne 0)$$

那椭圆曲线长什么样子呢，百闻不如一见，图片能直观感受。

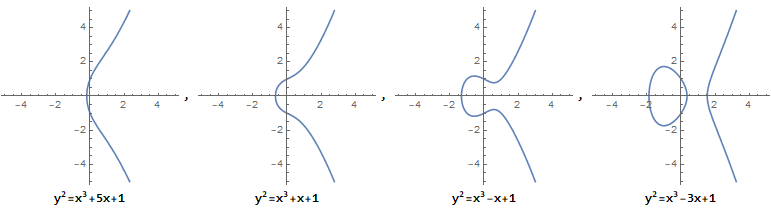
为什么需要满足 $4a^3+27b^2\ne 0$ 呢？因为当这个公式等于 0 时，它不是椭圆曲线。

SM2 公私钥

算法是基于数学的，SM2 定义曲线上的群运算加减乘，通过公私钥的生成理解。结合下面这张图，我们了解一下 SM2 的几何意义，了解什么是倍点运算。

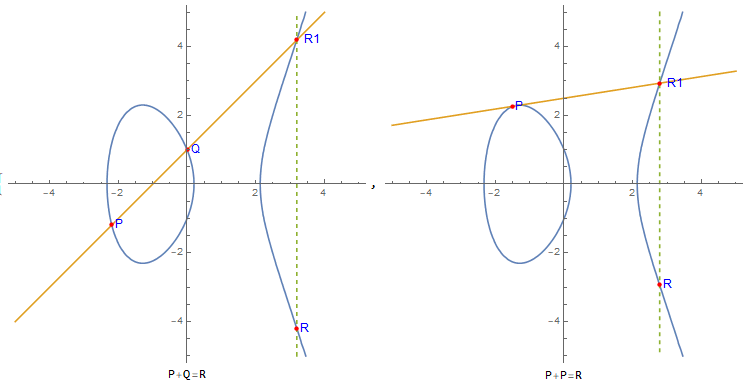
1. 首选一条椭圆曲线，即固定公式 $y^2=x^3+ax+b$ 中 a、b 的值，假设选择的是上图所示曲线。
2. 随机选择一个点 P 为基点，曲线做切线，经过 Q 点，切点 R1。
3. 基于 x 轴做 R1 的对称点 R，则 SM2 定义加法为 P + Q = R，这就是椭圆曲线加法。
4. 求 2 倍点，当 P = Q 时，即 P + P = R = 2P，则 R 是 P 的 2 倍点。
5. 求 3 倍点，3P = P + 2P = P + R，经过 P、R 做直线，交于椭圆曲线点 M1, 基于 x 轴对称点 M 则是 3 倍点，依次类推。
6. 求 d 倍点，假设我们同样次数为 d，运算倍点为 Q。
7. d 为私钥，Q 为公钥。所以私钥是一个大整数，公钥是一个点坐标。

上面的几何推理是为了方便理解，实际取值都是在质数有限域上。密码专家们经过推理和运算，已经为我们选择了质数有限域上的最优椭圆曲线，除非有特殊需要，否则不需要自定义曲线。

SM2 推荐曲线

• p：椭圆曲线在质数 p 的有限域 Fp 上的点集合；

• a：椭圆曲线参数 a 的值；

• b：椭圆曲线参数 b 的值;

• n：取值范围，随机整数 d 的取值范围 $[1,n-2]$；

• Gx：基点的 x 坐标值，类似于点 P 的 x 坐标值；

• Gy：基点的 y 坐标值，类似于点 P 的 y 坐标值。

SM2 加密

SM2 加密结果长度是固定的，例如密码为 123456 的 6 位数字，加密后密文长度 = 64 + 32 + 6 = 102 字节，转为 16 进制字符串结果为 204 个字符。原文长度为 n，则加密结果长度 $r=96+n$。

加密过程：

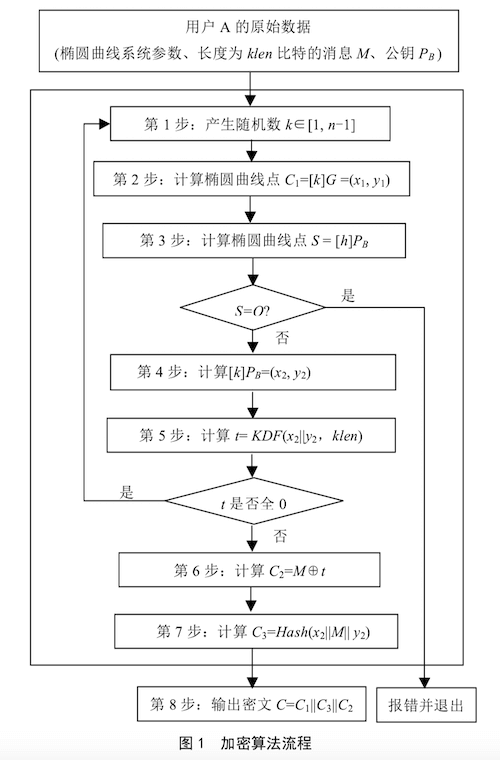
设椭圆曲线为推荐曲线，公钥 Q，原文比特串 M，klen 为 M 的比特长度；

1. 计算随机椭圆曲线点 $C1=[k]G=(x1,y1)$，k 是随机数，G为基点，计算出的倍点 C1 为 64 字节；
2. 校验公钥 Q，计算椭圆曲线点 $S=[h]Q$，h为余因子，若S 为无穷点，退出；
3. 计算椭圆曲线点 $[k]PB=(x2,y2)$，获取 x2，y2；
4. 计算 $t=KDF(x2||y2，klen)$，若 t 为全 0 比特串，则返回步骤 1，KDF是 SM2 的密钥派生函数;
5. 计算 $C2=M\oplus t$，对明文加密，C2 是真正的密文，长度和原文相同；
6. 计算 $C3=Hash(x2||M||y2)$，生成杂凑值，用来效验数据，长度 32 字节；
7. 输出密文 $C=C1||C3||C2$，C 为密文结果。

注意

OpenSSL 加密结果是经过 ASN1 格式化编码的，加密结果长度会不固定。加过过程中使用了随机数，所以每次加密结果都不一样。

SM2 解密

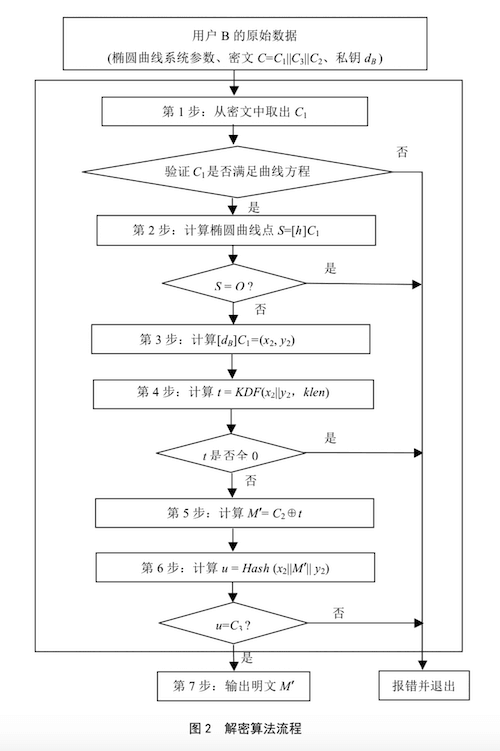
SM2 解密就是逆流程走一遍，注意 OpenSSL 解密要求传入的密文是 ASN1 编码的。

设椭圆曲线为推荐曲线 私钥 d，密文 C（$C=C1||C3||C2$），klen 为密文中 C2 的比特长度。

1. 从 C 中取出比特串 C1（密文 C 的前 64 字节），将 C1 的数据类型转换为椭圆曲线上的点，验证 C1 是否满足椭圆曲线方程，若不满足则报错并退出;
2. 计算椭圆曲线点 $S=[h]C1$，若 S 是无穷远点，则报错并退出；
3. 计算$[d]C1=(x2,y2)$，将坐标 x2、y2 的数据类型转换为比特串；
4. 计算 $t=KDF(x2||y2，klen)$，若 t 为全 0 比特串，则报错并退出；
5. 从 C 中取出比特串 C2，计算 $M^{\prime }=C2\oplus t$；
6. 计算 $u=Hash(x2||M^{\prime }||y2)$，从 C 中取出比特串 C3（密文 C 的后 32 字节），若 $u\ne C3$，则报错并退出；
7. 输出明文 M'，M' 就是解密后的明文。